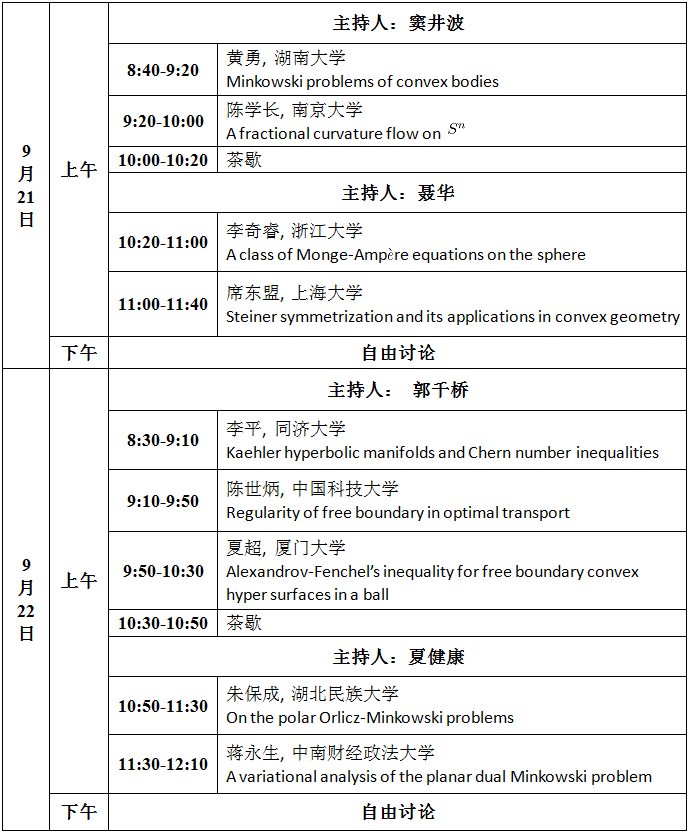
日程安排:
报告题目及摘要
Regularity of free boundary in optimal transport
陈世炳 中国科技大学
Free boundary arises in optimal transport problem when only a portion of mass is transported. In an important paper Caffarelli and McCann established the 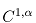 regularity of the free boundary assuming the domains are strictly convex and disjoint. In this talk I will present our recent slight improvement on this result by relaxing the "strict convexity" condition on the domains to the usual convexity, thus making this regularity result sharp. This is based on a joint work with Jiakun Liu.
regularity of the free boundary assuming the domains are strictly convex and disjoint. In this talk I will present our recent slight improvement on this result by relaxing the "strict convexity" condition on the domains to the usual convexity, thus making this regularity result sharp. This is based on a joint work with Jiakun Liu.
A fractional curvature flow on 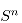
陈学长 南京大学
We first recall some techniques of scalar curvature flow on 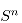 developed in my previous paper joint with Professor Xingwang Xu (Invent. Math. 2012). Next, we extend such a flow approach to prove a perturbation result of the fractional Nirenberg problem, i.e. prescribing fractional Q-curvature problem on
developed in my previous paper joint with Professor Xingwang Xu (Invent. Math. 2012). Next, we extend such a flow approach to prove a perturbation result of the fractional Nirenberg problem, i.e. prescribing fractional Q-curvature problem on 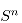 for
for 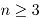 and the fractional exponent
and the fractional exponent 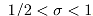 . This is joint with Pak Tung Ho and Jingang Xiong.
. This is joint with Pak Tung Ho and Jingang Xiong.
Minkowski problems of convex bodies
黄 勇 湖南大学
In this talk, I will report briefly on the development of Minkowski problems of convex bodies. In particular, I will also discuss some new geometric measures and their characterisation problems in the Brunn-Minkowski theory, which is a joint work with Prof. E. Lutwak, D. Yang and G. Zhang.
A variational analysis of the planar dual Minkowski problem
蒋永生 中南财经政法大学
We give a variational analysis to the planar dual Minkowski problem in Sobolev space. With the new variational characterization, we can deal with existence results for prescribed not necessarily positive data. Meanwhile, functional inequalities and multiple solutions are also obtained.
Kaehler hyperbolic manifolds and Chern number inequalities
李平 同济大学
In this talk we review a well-known conjecture due to Hopf and Chern, and explain their solution in the Kaehler case due to Gromov via the notion of "Kaehler hyperbolicity". Then we shall report our recent work around Kaehler hyperbolic manifolds.
A class of Monge-Ampere equations on the sphere
李奇睿 浙江大学
There are a number of geometric problems which can be reduced to the study of Monge-Ampere equations on the sphere, including the Aleksandrov problem, the Minkowski problem, and the 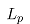 dual Minkowski problem introduced recently. In this talk we give a brief discussion on these problems.
dual Minkowski problem introduced recently. In this talk we give a brief discussion on these problems.
Steiner symmetrization and its applications in convex geometry
席东盟 上海大学
Steiner symmetrization was introduced by Steiner in the 18th century. Many (affine) isoperimetric inequalities in convex geometry that characterize ellipsoids can be established by using this approach. In this talk, we will present some new developments and applications of Steiner’s approach, including the affine inequalities for sets of finite perimeter, and general affine invariances related to Mahler volume.
Alexandrov-Fenchel’ s inequality for free boundary convex hypersurfaces in a ball
夏超 厦门大学
In this talk, we study free boundary convex hypersurfaces in a ball. A suitablequermassintegral will be introduced in this setting. In particular, the highest oder quermassintegral is a topological constant by Gauss-Bonnet-Chern’s formula. We will establish a family of Alexandrov-Fenchel’s inequalities by using a locally constraint inverse type curvature flow. This is a joint work with Julian Scheuer and Guofang Wang.
On the polar Orlicz-Minkowski problems
朱保成 湖北民族大学
We will talk about the polar Orlicz-Minkowski problems: under what conditions on a nonzero finite measure 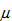 and a continuous function
and a continuous function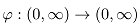 there exists a convex body
there exists a convex body 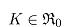 such that is an optimizer of the following optimization problems:
such that is an optimizer of the following optimization problems:
.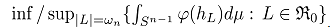
The solvability of the polar Orlicz-Minkowski problems is discussed under different conditions. In particular, under certain conditions on 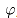 , the existence of a solution is proved for a nonzero finite measure
, the existence of a solution is proved for a nonzero finite measure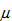 on unit sphere
on unit sphere 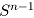 which is not concentrated on any hemisphere of
which is not concentrated on any hemisphere of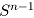 .
.
.




 当前位置:
当前位置: